量子少体问题一直以来是核物理领域一项重要的研究内容，近年来随着超冷原子系统实验和理论的迅速发展，它在冷原子领域得到越来越多的关注，成为实验和理论研究的一大热点。其研究意义在于：
　　一方面，对于冷原子这样一个极其稀薄的系统，少体问题的研究不仅是建立一个多体相互作用模型的基本依据，而且对多体系统的性质有重要的启示作用。它的求解是实现散射共振，制备强关联多体系统的必经手段，同时对实验上控制原子损失率和保持原子气体的稳定性都有重要的现实意义。
　　另一方面，少体物理也可以展现其所特有的量子效应。一个典型的例子是三体Efimov态。1970年，俄国核物理学家Efimov预言三个可分辩粒子在两体共振散射时所形成的无穷多数目的束缚态，且其束缚能有分立标度不变性。它的第一个实验验证则是2006年由Innsbruck小组在铯原子气体中完成的。从更广的范围看，Efimov态是Borromean环的一种，这一类物态的标志特征是只有三个粒子会形成束缚态（环链），而其中任意两个都不互相束缚（Fig.1）。这是一个纯粹由量子力学导致的效应，有丰富而深刻的物理内涵。
　　近年来自旋轨道耦合在超冷原子气体中的实现为量子少体问题的研究提出了新的挑战。这一挑战源于自旋轨道耦合所导致的两大效应：一是它将具有不同轨道角动量的散射通道耦合在一起，使得通常的分波散射方法不再适用；二是它有效地改变了低能态空间及态密度，因此需要对低能空间的散射作重新考量。这两大效应必将会对少体系统的性质产生重要影响，而目前自旋轨道耦合的冷原子系统中少体物理的研究还几乎处于空白，许多未知问题亟待研究解决。最近，中科院物理研究所/北京凝聚态物理国家实验室（筹）凝聚态理论与材料计算实验室崔晓玲研究员与清华大学翟荟研究员和博士生史哲雨，以及中国科学技术大学易为教授合作，在自旋轨道耦合超冷原子气体的少体问题这一热点领域取得了一系列重要研究进展。
　　他们首先考虑两个较重的费米子与一较轻的带自旋轨道耦合的粒子有相互作用的体系。发现由于不同轨道角动量之间的耦合效应，三体基态能量会进一步降低，从而在更大的质量比及相互作用参数区间有三体束缚态的存在（Fig.2）。这些三体束缚态的出现同时伴随着原子-分子之间的散射共振，从而使得自旋轨道耦合成为一个新的可操控散射共振的有效手段，对冷原子体系的多体性质以及其三体损失率及稳定性有重要影响。此成果发表于Phys. Rev. Lett. 112, 013201 (2014).
　　他们进一步研究发现，自旋轨道耦合还可以在没有两体分子态的基础上诱导出三体束缚态，即Borromean态（Fig.1)。这可以通过对三体系统中的两个费米子施加一个具有高度对称性的自旋轨道耦合（例如Rashba类型）来实现。不同于以往研究中的Borromean态，这里它的出现不依赖于两体相互作用势的具体细节，而只与s波散射长度（代表有效长程作用）和自旋轨道耦合强度有关系，因此具有普适性（Fig.3）。这也是首次发现有普适性Borromean态的物理系统，大大方便了对这种奇异的量子少体态的实验探测。其存在的本质原因在于自旋轨道耦合极大地增强了三体的低能散射相空间而有效抑制了两体散射，从而使得三体比两体更容易形成束缚态（Fig.4）。这也意味着一个多体系统中三体关联更强于两体关联，从而可以诱导出更新奇的量子多体态。这一研究结果揭示了单粒子能谱对称性在少体物理中起的关键作用，对在一般系统中探索更奇异的少体态和少体关联有重要启示。这一成果发表在近期出版的Phys. Rev. X 4, 031206 (2014), 并在Physics上被重点介绍（见以下链接）。
　　该工作得到了国家自然科学基金等项目支持。
　　文章链接：　http://dx.doi.org/10.1103/PhysRevLett.112.013201
　　　　　　　　http://dx.doi.org/10.1103/PhysRevX.4.031026
　　　　　　　　http://physics.aps.org/synopsis-for/10.1103/PhysRevX.4.031026

Fig.1: Borromean环。只有三体才可相互束缚，其中任意两体都不构成束缚。

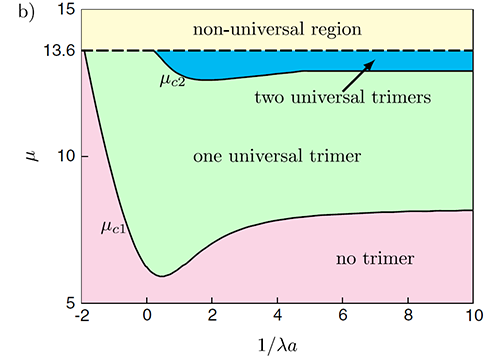Fig.2：三体束缚态随质量比（纵轴），自旋轨道耦合及s波散射长度（横轴）变化的相图。粉红色区域原子-分子态能量较低，其它区域三体束缚态能量较低。相较于无自旋轨道耦合情况，此处三体束缚态可存在于更低的质量比以及负的散射长度区间。

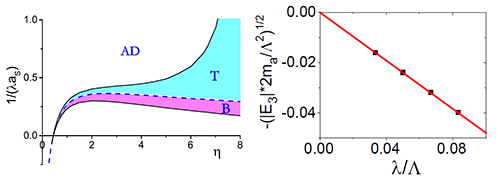Fig.3: （左）三体束缚态能量随高能截断动量的关系。图中的y-x线性依赖说明其能量并不依赖于高能或短程物理，因此其对于不同的短程相互作用势具有普适性。 （右）三体系统的基态随质量比（横轴），Rashba自旋轨道耦合及s波散射长度（纵轴）变化的相图。“B”代表Borromean态，“T”代表有分子态存在时的三体束缚态，“AD”代表原子-分子态。

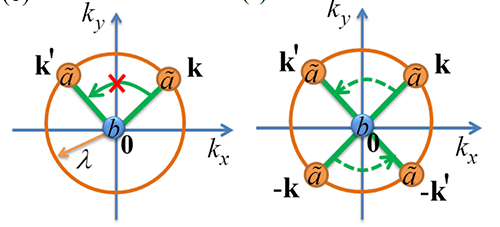Fig.4: Borromean态原理图。橙色圆环代表由Rashba自旋轨道耦合导致的a粒子的U(1) 基态简并。无自旋轨道耦合的b粒子基态处于零动量。对于a-b两体散射(左图)，不同基态动量间散射因总动量守恒条件被抑制；而对于a-a-b三体散射（右图），不同基态动量对之间的散射被允许，说明三体散射的低能相空间要远大于两体散射，从而有利于Borromean态的形成。