上世纪七十年代,物理学家费曼问一位年轻的同事:如果孤身去一个未知的险境,而只能携带一个日常工具,你的选择是什么?年轻同事的答案是:瑞士军刀,而费曼自己的选择是:计算器!骄傲如费曼,也许想到,他还是需要一个小小计算器,才能独力重构现代科学的大厦。 不过很快他就改变了主意,八十年代初,费曼指出,经典计算机并不是一个解决量子问题的有效工具,世界是量子的,一个简单的包含几十个粒子的量子系统,就超越了经典计算机的计算和存储能力,所以我们需要一台量子计算机,一个按照量子力学原理运行的计算机。援古证今,在中国古代用算盘的时期,人们无法想象计算机会有什么用,而现在我们也面临同样的问题,量子计算机我们需要吗?它能做什么?经过多年研究,人们已经提出了诸多量子算法,指出量子计算机可以解决或虚拟或现实、或过去或未来的各种经典问题。费曼设想的场景也许是随着量子技术的发展,人们将会碰到越来越多需要解决的量子工程问题,量子计算机无疑是解决量子问题的有效工具。
利用一个可操控的量子系统去模拟复杂的量子现象或者解决经典计算机难以解决的量子问题是量子计算的重要应用。近年来,随着可集成量子比特数的增多,相干时间的延长,以及操控和读出精度的提升,超导量子计算成为量子模拟的重要平台之一。运用经典计算机准确模拟量子多体系统的非平衡性质是人们长期关注的课题,而运用超导量子计算平台模拟非平衡性质为研究这一类问题提供了新途径。 动力学相变这一概念是非平衡动力学领域一直以来的研究热点,第一类动力学相变关注非平衡序参量,第二类动力学相变则与时间域上洛施密特回波(Loshmidt echo)的非解析性以及统计物理里的李-杨零点存在紧密联系,最近的理论与数值研究表明这两类动力学相变可以纳入同一框架进行研究。
近年来,中国科学院物理研究所/北京凝聚态物理国家研究中心与浙江大学在超导量子计算研究方面合作紧密。近期,物理所许凯副研究员、博士生孙政杭、郑东宁研究员、范桁研究员与浙江大学物理系博士生刘武新、李贺康博士、王浩华教授等,以及日本理化学研究所张煜然博士、野理(F. Nori)教授合作团队,利用16个超导量子比特实现了动力学相变的量子模拟,成果于近日在国际学术期刊《Science Advances》发表。
在此工作中,合作团队利用前期20量子比特薛定谔猫态工作中所研发的全联通超导多量子比特器件(图一),通过给超导量子比特施加一个同等振幅和相位的可控横场驱动,实现了Lipkin-Meshkov-Glick模型。该模型具有理论可预测的动力学相变现象,器件的多联通性质及驱动场调控可与模型及其参数相对应。实验首先展示了第一类动力学相变(图二)。在动力学铁磁相中(此时横场强度较弱),磁化率随时间的演化较为缓慢,磁化率的时间平均为有限值,破坏了Z2全局对称性;与之相反,在动力学顺磁相中(此时横场强度较强),磁化率的时间平均值为0且具有Z2全局对称性。之后,通过测量洛施密特回波的时间演化,实验验证了在动力学顺磁相中存在洛施密特回波的零点,而在动力学铁磁相中,短时间内的洛施密特回波为有限值。上述实验结果间接揭示了这两类动力学相变之间的联系(图三)。最后,通过对多比特量子态自旋压缩性质的测量,揭示了动力学相变临界点和自旋压缩态产生的直接关联。通过测量不同横场强度下自旋压缩系数的时间演化,发现动力学相变临界点附近的自旋压缩最为显著,测得的压缩系数体现了多体真纠缠的存在,这一结果揭示动力学相变在量子精密测量领域的潜在应用(图四)。
展望:量子模拟现在完成的任务还处于现有计算机的计算范围之内,而实验的主要目的也是展示量子计算平台可以按照人们预期的量子力学原理运行,而随着量子比特数的增长,将来的量子模拟将可以完成经典计算机所不能预测和检验的任务,其作用将不可替代。
此工作得到国家重点研发计划(No. 2017YFA0304300,No. 2016YFA0300600),自然科学基金(No. 11934018, No. 11725419,No. 11904393)以及中科院B类先导专项(No. XDB28000000)等基金的支持。
本文的同等贡献一作为:许凯(中科院物理所)、孙政杭(中科院物理所)、刘武新(浙江大学),通讯作者为:郑东宁(中科院物理所)、范桁(中科院物理所)、王浩华(浙江大学)。
参考文献:
Kai Xu#, Zheng-Hang Sun#, Wuxin Liu#, Yu-Ran Zhang, Hekang Li, Hang Dong, Wenhui Ren, Pengfei Zhang, Franco Nori, Dongning Zheng*, Heng Fan*, H. Wang*,
Probing dynamical phase transitions with a superconducting quantum simulator,
Science Advances 6, eaba4935 (2020).
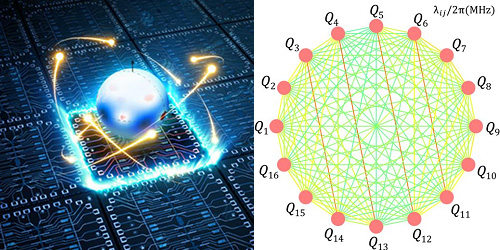
图一:左图为实验所用制备20量子比特薛定谔猫态时的器件概念图,这次实验选取了其中16个量子比特,这16个量子比特间的相互作用大小如右图所示。
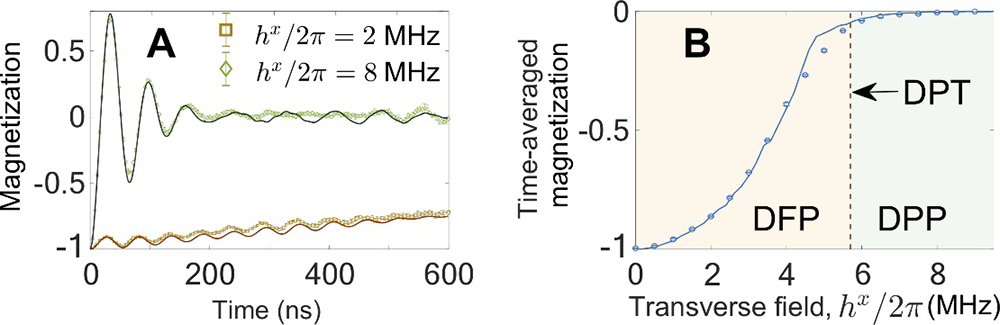
图二:A磁化率的时间演化。横场强度为2MHz时,系统处于动力学铁磁相(DFP),而当横场强度为8MHz时,系统处于动力学顺磁相(DPP)。B磁化率的时间平均与横场强度的关联。实验结果与理论预测的动力学相变(DPT)点位置(由图中虚线标示)吻合。
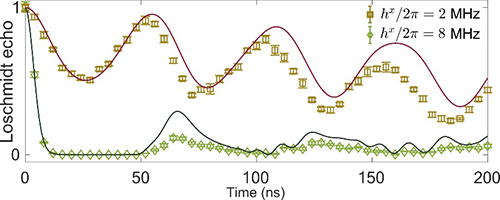
图三:洛施密特回波在动力学铁磁相和顺磁相中的时间演化行为。
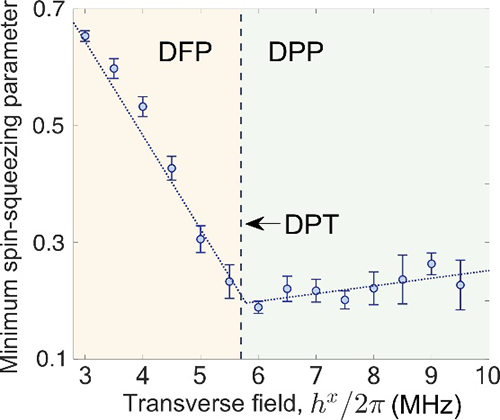
图四:时间域上自旋压缩系数的最小值随横场强度的变化。